Función cuadrática

En matemáticas, una función cuadrática es una variable de una función polinómica definida por:

${\displaystyle y=ax^{2}+bx+c\,}$

con ${\displaystyle a\neq 0}$.¹​ También se da el caso que se le llame Trinomio cuadrado perfecto.²​ También se denomina función cuadrática a funciones definidas por polinomios cuadráticos de más de una variable, por ejemplo:

${\displaystyle f(x,y)=Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F}$

En este caso el conjunto de puntos que resultan al igualar el polinomio a cero representan lugares geométricos que siempre es posible reducir a una de las formas:

${\displaystyle \left({\frac {x}{a}}\right)^{2}\pm \left({\frac {y}{b}}\right)^{2}=c^{2},\qquad \left({\frac {x}{a}}\right)^{2}\pm {\frac {y}{b}}=c}$

Que corresponden a tres tipos de secciones cónicas (elipse, hipérbola y parábola).

as gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").

El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, por ejemplo la caída libre o el tiro parabólico.

La derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.

EN EL DEPORTE 

Trayectorias. En cualquier deporte en el que se observa un tiro (fútbol, baloncesto, rugby, etc…), este describe una trayectoria parabólica, cuya representación gráfica en matemáticas es la parábola (del griego παραβολή), que es la sección cónica resultante de cortar un cono recto con un plano paralelo a su generatriz. Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta (eje o directriz) y un punto fijo llamado foco. La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del movimiento de los cuerpos bajo la influencia de la gravedad. La tradición dice que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo, donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes. Sin embargo, el primero en usar el término parábola fue Apolonio de Perge en su tratado Cónicas, considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas. Es Apolonio quien menciona que un espejo parabólico refleja de forma paralela los rayos emitidos desde su foco, propiedad usada hoy en día en las antenas satelitales. La parábola también fue estudiada por Arquímedes, nuevamente en la búsqueda de una solución para un problema famoso: la cuadratura del círculo, dando como resultado el libro Sobre la cuadratura de la parábola. Desde el punto de un punto de vista de la física podemos descomponer una trayectoria parabólica en un movimiento rectilíneo uniforme (eje x) y un movimiento rectilíneo uniformemente acelerado (eje y). En estos movimientos, consideramos que la gravedad es la única fuerza que actúa. Si un cono es cortado por un plano a través de su eje, y también es cortado por otro plano que corte la base del cono en una línea recta perpendicular a la base del triángulo axial, y si adicionalmente el diámetro de la sección es paralelo a un lado del triángulo axial, entonces cualquier línea recta que se dibuje desde la sección de un cono a su diámetro paralelo a la sección común del plano cortante y una de las bases del cono, será igual en cuadrado al rectángulo contenido por la línea recta cortada por ella en el diámetro que inicia del vértice de la sección y por otra línea recta que está en razón a la línea recta entre el ángulo del cono y el vértice de la sección que el cuadrado en la base del triángulo axial tiene al rectángulo contenido por los dos lados restantes del triángulo. Y tal sección será llamada una parábola Apolonio de Perge 7 Si se lanza un balón desde una altura h sobre un plano horizontal con velocidad inicial v0, haciendo un ángulo con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura. Que viene definida en función del tiempo por las fórmulas: Las componentes de velocidad en función del tiempo de la trayectoria del balón, sería: En una trayectoria podemos definir el tiempo de vuelo que permanece el balón en el aire como: También podemos obtener el alcance máximo que alcanzará la pelota. Para calcular la altura máxima que alcanza el balón se utiliza.

APLICACIONES DE LAS FUNCIONES EN ARQUITECTURA

En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el rango).

Para hacer edificios más seguros y precisos, la arquitectura utiliza especialmente las funciones trigonométricas; ya que permite al arquitecto calcular las distancias y las fuerzas relacionadas con elementos de la diagonal.
De las funciones trigonométricas básicas, el seno, el coseno y la tangente son los más importantes para la arquitectura, ya que permiten al arquitecto encontrar fácilmente los valores opuestos y adyacentes relacionados con un ángulo o la hipotenusa.

Triángulo Rectángulo
Funciones trigonométricas seno, coseno y tangente.

Gráficas de funciones trigonométricas

La trigonometría  se utiliza mucho en la arquitectura moderno, tanto que ésta es incompleta sin la otra. Las formas de gran estrella en los edificios, hermosas estructuras curvas de acero, piedra, vidrio entre otras, no serian posibles sin el uso de la trigonometría. En realidad los paneles planos y planos rectos en los edificios se encuentran en un ángulo entre sí y la ilusión que tenemos es la de una superficie curva. Incluso mientras se decide el interior de los hogares y oficinas, la trigonometría juega un papel vital.
También puede ser utilizada en la arquitectura como es en la construcción de edificios así también como en la construcción de túneles a través de montañas y calcular la dirección para que el túnel salga al otro lado en el lugar deseado.

EJEMPLOS:

Teatro Popular en Niterói
Para el diseño de este edificio se utilizó una función trigonométrica, ya que si ubicamos la forma de este edificio en un plano cartesiano, tomando en cuenta que la punta de lado izquierdo del edifico pasa por el origen del plano cartesiano, con esta información podemos deducir el edifico pertenece a la función de Seno. El teatro Popular fue diseñado por el arquitecto Oscar Niemeyer en el año 2007.

Bridge of Peace
Al igual que la imagen anterior la forma de este puente pertenece a una función trigonométrica. Si localizamos este diseño en un plano cartesiano podemos ver que el inicio del puente pasa por la coordenada (0,1) con esto podemos deducir que la silueta de este puente pertenece a la función coseno.
Este símbolo contemporáneo diseñado por el arquitecto Michele de Lucchi a principios de 2010. Tiene 150 m de largo y se encuentra ubicado en Georgia.

REPORT THIS AD

Zentrum Paul Klee
Esta obra representa claramente la aplicación de las funciones trigonométricas en la arquitectura.
En esta obra se utilizó la función seno, ya que la silueta del edificio colocado en un plano cartesiano, nos demuestra que el contorno del edifico pasa por el origen del plano, lo cual nos indica que este edificio se aplicó la función seno.
Esta obra fue diseñada por el arquitecto suizo Renzo Piano y el artista Paul Klee, en conjunto diseñaron el edificio Zentrum Paul Klee en 1999.

---

Funciones Cuadráticas

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

• f(x) = ax² + bx + c

El vértice es un indicador importante del punto máximo o mínimo alcanzado. Estas funciones también se representan como texto, tablas de valores y fórmulas.

En arquitectura, se emplean las funciones cuadráticas mayoritariamente para la construcción de puentes colgantes que tienen que soportar un peso uniformemente distribuido.

---

Funciones Exponenciales

La función exponencial es del tipo:

• f(x)=ax

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.

En arquitectura, se puede asociar este tipo de funciones para la planificación del desarrollo urbano de una ciudad.

EN LA FISICA

   El estudio de la ecuación cuadrática en el contexto de la física sirve como una plataforma para establecer conexiones de los conceptos fundamentales de la ecuación cuadrática. De esta manera se asocian aspectos de la ecuación cuadrática con el tema de caída libre de los cuerpos, mostrando como se puede transitar de un contexto a otro con la finalidad de lograr la comprensión de los conceptos matemáticos

Palabras clave: Ecuación, cuadrática, raíz, caída libre.

Abstract

The study of the quadratic equation in the context of physics serves as a platform to establish connections of the fundamental concepts of the quadratic equation. By this way, the aspects of the quadratic equation are associated with the issue of free falling bodies, showing how you can move from one context to another in order to develop the comprehension of mathematical concepts.

Keywords: Equation, square root, freefall.

ESTUDIO DE LA ECUACIÓN CUADRÁTICA EN EL CONTEXTO DE LA FÍSICA

En el estudio de cualquier tema matemático es importante que se plantee la búsqueda de conexiones y relaciones en áreas diferentes al de las matemáticas, de manera que se facilite el entendimiento y significado de los conceptos fundamentales al relacionarlos con otros contenidos (NCTM, 2000).

De esta manera, al conectar la ecuación cuadrática en el contexto de la física, se pueden identificar y aplicar conceptos matemáticos en un área distinta.

En este sentido Schoenfeld (citado en Santos, 1997), sugiere que para entender conceptos matemáticos, es necesario proponer actividades que ayuden a los estudiantes a discutir los conceptos en diferentes contextos.

Bajo esta visión, se pueden relacionar aspectos generales de caída libre de los cuerpos con aspectos fundamentales de la ecuación cuadrática, ya que dichas ecuaciones cuadráticas juegan un papel importante en el área de la física.

El movimiento de caída libre es un movimiento uniformemente acelerado, es decir, la aceleración instantánea es la misma en todos los puntos del recorrido y coincide con la aceleración media, y esta aceleración es la aceleración de la gravedad g = 9,8 m/seg2.

Un objeto en caída libre experimenta una aceleración de 9.8 m/seg2 (negativo) indicando una aceleración hacia abajo, de esta manera si un objeto cae de una cierta altura, la velocidad inicial del objeto es 0 m/seg.

Es importante considerar que la ecuación que permite calcular la distancia de un cuerpo en caída libre corresponde a la siguiente ecuación cuadrática:

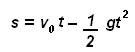
Debemos considerar, que la distancia s en la ecuación anterior representa el desplazamiento hacia abajo del origen. Si ses negativo, indica un desplazamiento por debajo del punto de partida.

Por ejemplo:

Se deja caer un objeto desde la azotea de un edificio, como se muestra en la figura 1, dada su velocidad inicial igual a cero, encontrar su posición o distancia desplazada hacia abajo después de 0 seg., .5 seg., 1 seg., 1.5 seg., 2 seg., 2.5 seg., 3 seg.

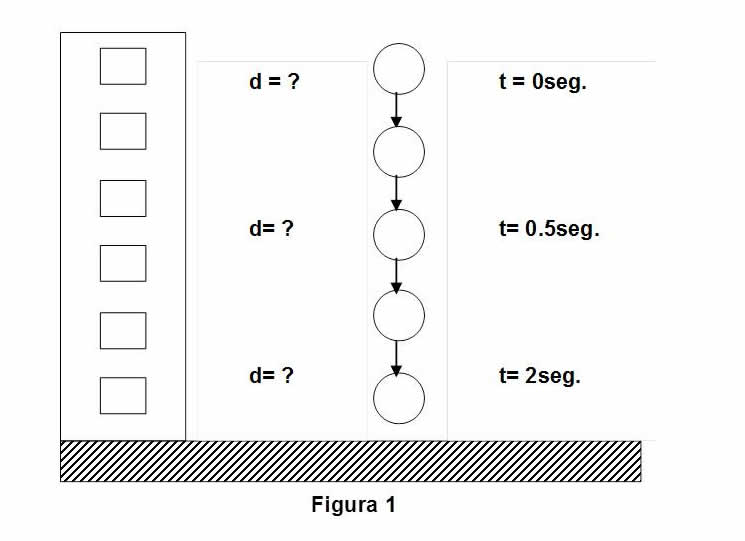
Entonces la posición como función del tiempo se calcula a partir de la ecuación

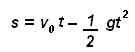
Debido a que la velocidad inicial es cero, y la aceleración de la gravedad es (-9.8 m/seg2) ya que el desplazamiento del cuerpo es hacia abajo; entonces podemos calcular la distancia en función del tiempo a partir de la ecuación cuadrática anterior, y tenemos:

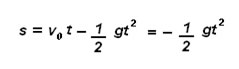
Entonces:

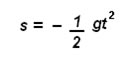
A partir de la función cuadrática anterior podemos calcular la distancia recorrida por el cuerpo en caída libre.

Después de 0 seg., el cuerpo caerá a una distancia de:

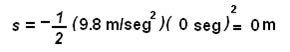
Después de 1 seg., el cuerpo caerá a una distancia de:

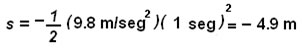
En forma similar se obtiene las demás distancias después de 1.5, 2, 2.5 y 3 segundos respectivamente.

En la siguiente tabla se muestran los datos calculados:

TIEMPO  (segundos)	DISTANCIA (metros)
3.00	-44.10
2.50	-30.63
2.00	-19.60
1.50	-11.03
1.00	-4.90
0.50	-1.23
0.00	0.00

Tabla 1

Con los datos anteriores, podemos obtener la gráfica de la función asociada a la ecuación cuadrática que calcula la distancia, es importante considerar que el signo negativo de la distancia indica el desplazamiento del objeto hacia abajo.

La gráfica de una función cuadrática corresponde a una parábola, la cual puede intersecar uno, dos o ningún punto del eje horizontal, de esta manera podemos deducir que al graficar los datos mostrados en la tabla 1 obtendremos una curva correspondiente a la función cuadrática:

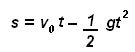
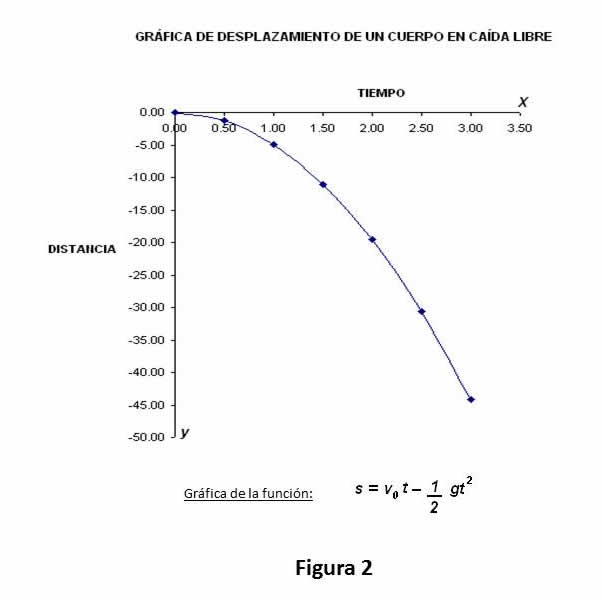
En la gráfica de la función cuadrática de la figura 2 podemos observar que la gráfica interseca al eje x en el punto (0,0), por tanto las raíces de la ecuación cuadrática corresponden a x1= 0 y x2=0; y se pueden asociar o interpretar con el punto de partida donde se dejo caer el objeto.

Retomando así los conceptos fundamentales de la ecuación cuadrática, las raíces de una ecuación cuadrática son los puntos de intersección de la gráfica de su función cuadrática asociada con el eje x, lo cual nos permite mostrar de manera evidente que la ecuación que permite calcular la distancia de un cuerpo en caída libre es una ecuación cuadrática y que en el contexto de la física el concepto raíz también tiene una interpretación y significado.

De esta forma, aspectos relacionados con la ecuación cuadrática pueden ser abordados en otros contextos, mostrando de esta manera la conexión que guardan los conceptos y sus relaciones con otra disciplina.

Es claro, que en el contexto de la física, los conceptos fundamentales que emergen del estudio de la ecuación cuadrática también pueden ser conectados e interpretados con aspectos fundamentales de caída de los cuerpos, como se muestra en la figura 3.

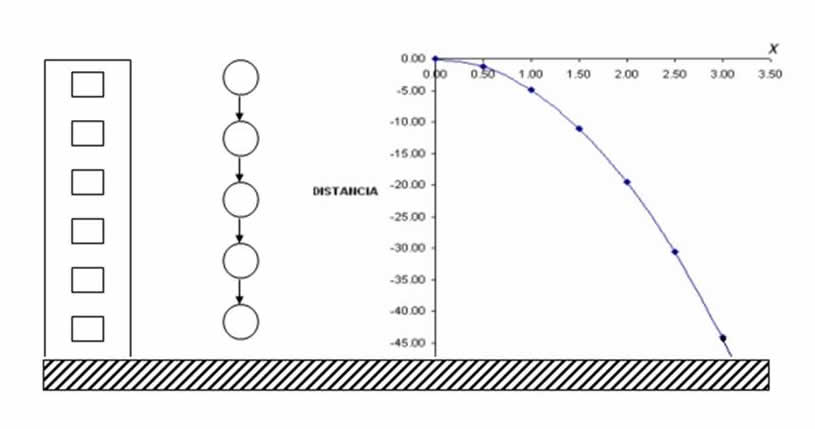
Figura 3 Muestra la gráfica de la distancia recorrida por un cuerpo que se dejo caer desde la azotea de un edificio.

En este sentido, las raíces en el contexto de la física pueden ser interpretadas, como el punto en donde se dejo caer un objeto o el punto de partida de dicho objeto, y en forma algebraica obtendríamos el valor de la raíces aplicando la formula general y determinar a partir del valor del discriminante que la grafica de la función cuadrática asociada interseca en un punto al eje x, teniendo así la ecuación cuadrática dos raíces iguales las cuales corresponden al punto de intersección de la gráfica de la función con el eje horizontal.

A partir de dicha interpretación podemos identificar las raíces en la grafica de la función cuadrática y considerando los datos proporcionados al calcular la distancia de desplazamiento de un cuerpo en caída libre darle un significado en el contexto de la física.

Es así, como los conceptos fundamentales de la ecuación cuadrática tienen conexión en el contexto de la física, por ejemplo: el concepto raíz en la representación gráfica lo podemos interpretar como los puntos de intersección de la gráfica con el eje horizontal, en la forma algebraica a través de la fórmula general obtener el valor de la raíces y determinar que la ecuación tiene dos raíces reales iguales y finalmente en el contexto de la física asociamos la representación gráfica y algebraica para interpretar que la raíces corresponden al punto donde se deja caer el objeto al referirnos a la caída libre de los cuerpos.

De esta manera se pueden contextualizar los conceptos matemáticos al abordar un tema en un contexto diferente al de las matemáticas, y de esta manera se pueden identificar conexiones en uno y otro contexto, lo cual no ocurrirá cuando únicamente existe la mecanización de fórmulas y memorización de conceptos.

Así, “Cuando los estudiantes pueden conectar ideas matemáticas, su comprensión es más profunda y duradera. Pueden ver conexiones matemáticas en la rica interacción entre los temas matemáticos, en contextos que relacionan las matemáticas con otras disciplinas y en sus propios intereses y experiencias. A través de una enseñanza que resalte la interrelación de las ideas matemáticas, no sólo aprenden la asignatura sino que también se dan cuenta de su utilidad” (NCTM, 2000).